The uninformed may perceive GPT-3’s output as mystical, but in reality, it relies solely on statistical analysis. GPT-3 uses the principles of probability to determine the likelihood of each word’s appearance through its training, and then selects the next word accordingly.
The GPT-3 playground provides insight into the inner workings of this seemingly magical entity. You can reveal the top five potential words and their associated probabilities by enabling the ‘Show Probabilities’ setting, offering a glimpse into the calculations driving this model’s output.

GPT3 playground with the Show Probabilities setting turned on to full spectrum.
“Show Probabilities” displays the probability of the top 5 words, with the selected word highlighted in red. The word selected is determined by the temperature setting, where a setting of 0 will result in the top probability word being selected.
While the playground presents our results as percentages, GPT3 relies on a different mathematical approach to achieve computational efficiency.
Logarithmic Probabilities, or logprob, uses logarithmic mathematics to convert the percentage into a computationally manageable number. This article delves into the intricacies of logprob and the mathematical principles that drive it.
Intended Audience
This writing is aimed at Ruby developers, particularly those fascinated by the realm of Machine Learning, eager to delve deeper into the mathematical intricacies behind GPT3 and attain a fine-grained level of control over the model’s output.
For those fluent in Ruby, the article offers a unique opportunity to witness the concepts in action through code samples written in the Ruby language.
Prerequisites
Before delving into the heart of this piece, it is important to possess a foundation in:
The fundamental principles of the Ruby programming language,
A sound grasp of mathematics including exponentials and logarithms, and
The ability to interface with the OpenAI API.
In this piece, we delve into the heart of logarithms, exploring the mathematical underpinnings that power some of the most intriguing computational systems.
By leveraging the Math module, we will demonstrate the practical application of these principles in the context of the Ruby programming language. It is worth noting that, as a component of the core language, the Math module is readily available for use and does not need to be imported with require.
Overview of GPT3 Token Selection
GPT operates on a linguistic unit known as a token, which is comprised of a sequence of characters that can represent a full word or a fragment of a word. These tokens are derived from common character combinations that are observed across languages, and GPT’s vast database stores approximately 50,000 distinct tokens, each assigned a unique identifier, or token ID.
As an example, consider the word “untangle.” This word can be decomposed into two tokens: “unt” and “angle.” The token “unt” has been assigned the token ID of 1418, while “angle” bears the ID 9248.
To assist with tokenizing text, OpenAI has devised a tool referred to as the Tokenizer, which transforms text into a series of tokens and returns the corresponding token IDs.


Each token is given an ID based on its frequency in the training data provided to GPT-3. The lower the number, the higher the frequency during training.
OpenAI has estimated that a single token is equivalent to approximately four characters; however, this estimation is not always consistent. For instance, the word “ tomorrow” — with a space in front of it — is nine characters in total, yet it is still considered a single token.

It is a fascinating observation that the work “tomorrow”, without a leading space, is composed of two distinct tokens.

The power of GPT-3 lies in its ability to tokenize a prompt and use probability to determine the most likely proceding token. Tokens are affected by preceding spaces as well as capitalization.
To illustrate this, consider the simple example below in the GPT-3 playground with the temperature set to 0. This forces GPT-3 to select the highest probability token each time.
Are humans omnivores?
GPT will check its probability tables and find that based on its training data, the word “Yes” has a 99.99% probability of appearing next.

The period mark at the end of the response was also determined through probabilistic analysis. The model’s training data revealed that, given the response “Yes, humans are omnivores,” a period was the most likely character to follow with a probability of 84%.

The notion that GPT is anything more than a probability model, something akin to sentience, has been gaining traction on Reddit and other social networks of late. However, such a concept could not be further from the truth. GPT is nothing more than a sophisticated algorithm trained on an unfathomable amount of data — some 500 billion tokens of text, to be precise.
Through this dataset, GPT has learned to associate certain words and phrases with one another, to the point that it can generate text that mimics human language. Yet, for all its intelligence, GPT is still a long way off from being truly sentient.
A full list of GPT tokens can be found at the following link: https://github.com/latitudegames/GPT-3-Encoder/blob/master/vocab.bpe
How does GPT-3 use probabilities under the hood
The issue with probabilities is that performing operations on them is far from an efficient computing task, particularly when it comes to multiplication. Probability calculations often require multiplactive operations which are not computationally efficient. In stark contrast, addition is much more manageable computationally, with some systems seeing a tenfold reduction in processing time.
Let’s return to our prompt above:
Are humans omnivores?
GPT has tokenized this phrase into six tokens, each with its own probability. Each token is assigned a probability P1 — P6.

When GPT responds to the prompt above, it needs to determine the probability of the next token, which we can call P7. To do this, it needs to calculate the combined probability of all 7 tokens occurring in its training data. This can be done mathematically by multiplying the probabilities together, P1 P2 P3 P4 P5 P6 P7. However, as the response gets longer, the computational cost of this calculation increases exponentially.
In order to make this process more efficient, the OpenAI team turned to a method of probability invented in 1950 called Logarithmic Probability (logprob). Logprob allows computers to perform the same calculation using addition instead of multiplication, resulting in performance improvements. To gain a better understanding of Log Probability, you must first have a good grasp of logarithms.
Understanding Logarithms
Mathematics has long been the language of science, and logarithms stand as one of the most essential components of the discipline. As the inverse of exponentials, logarithms essentially undo the operations of the exponential function, much like subtraction undoes addition.
Inverse operations are most clearly demonstrated through an example: Start with the number 10, and add 5. The inverse operation in this case is to subtract 5, which undoes the addition and leaves us with 10 once more.
10 + 5 - 5
# Output: 10
In the same way logarithms are the inverse of exponentials.
Exponentials are mathematically operations which given a base tell us how many times to multiple that base by itself.

Represented in Ruby Code:
5**3
# Equivalent to:
5 * 5 * 5
#Output: 125
Exponential operations are useful in solving problems related to exponential grown such as compounding interest, or exponential decay such as radioactive half-life.

The exponential function illuminates the result of repeatedly multiplying a number by itself, while the logarithm reveals the number of such multiplications required to reach that result. In other words, the exponential describes the outcome of a process of repeated self-multiplication, while the logarithm reveals the number of such self-multiplications necessary to achieve that outcome.
The two concepts, therefore, exist in an intimate reciprocal relationship; the exponential informs us of the consequence of multiple self-multiplication, while the logarithm discloses the number of acts of self-multiplication necessary to attain the consequence.
Exponential: What is the result of multiplying 2 by itself three times.
2**3
#Output: 8
Logarithm: How many times do we need to multiple 2 by itself to get 8.
2 * 2 * 2
#Output: 8
The answer is 3. So the logarithm is 3.
In the following equation, x is the exponent, representing the number of times two is multiplied by itself to result in 8. In other words, x is the power to which two must be raised in order to achieve a product of 8.

In order to ascertain the value of x, we must apply the logarithmic formula.

The logarithmic equation can be expressed as follows: the logarithm of 8 with a base of 2. It is an indication of the number of times that 2 must be multiplied by itself to produce 8. The logarithm of 8 with a base of 2 is 3, meaning that 2 must be multiplied by itself 3 times in order to reach 8.
A good online tool for calculating logarithms is https://www.symbolab.com/

In Ruby, the Math module is capable of computing logarithms. By utilizing the Math.log method, one can easily calculate the logarithm of any given number. This method is defined as:
Math.log(result, base)
Where r is the result and b is the base.

Take the logarithic function below. We can use the log method to determine the number of times 2 needs to be multiplied by itself to get 8.

The logarithm of 8 with a base of 2.
Math.log(8, 2)
# Output: 3
The logarithmic graph stands in stark contrast to the exponential graph, a juxtaposition which becomes especially pertinent when considering the application of Logprobs. It is in fact this particular graph that furnishes the very foundation upon which Logprobs is predicated, thus enabling it to fulfill its vital purpose.
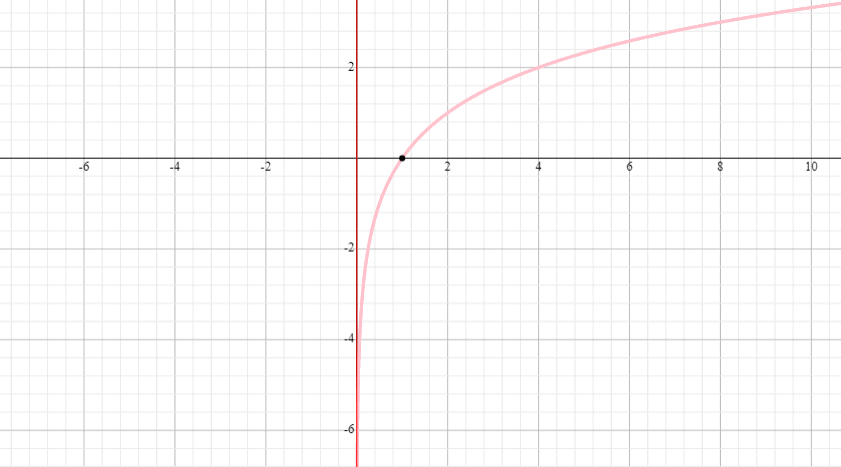
Natural Logarithms
In mathematics there is a concept of the natural logarithm. It is a specialised form of loagarith that makes use of the mathematical constant of e as a base.
This constant e is an omnipresent figure in a multitude of natural phenomena, such as compound interest, population growth, radioactive decay, spread of disease, and the decibel scale. The value of ‘e’ stands at approximately 2.71828. To gain a deeper understanding of its origin, the following video is a great place to start.
Here is an example of the natural log expressed mathematically.
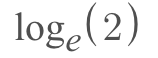
The formula above is asking what power do I need to raise e to in order to get 2.
The answer is 0.6934.
There is short-hand in mathematics for representing the natural logarithm.

The two formulas above represent the same expression. ln(2) is shorthand which means what is the power I need to raise e in order to get 2.
In Ruby the natural log is calculated using the log function by passing a single argument. If as additional second argument is given, it will be the base of logarithm. Otherwise the base is e by default.
Math.log(2)
# Output: 0.6931
How logarithms are used in probability calculations
Probabilities are expressed as a percentage, out of the maximum possible outcome of 100%, which signifies complete certainty. Computers, on the other hand, process probability percentages in decimal form. For example, 1 equates to 100%, 0.5 equates to 50%, and so forth.
Logarithms and probability have an interesting relationship: the graph of a logarithmic function is the key to understanding these two concepts in combination.

Observing the graph above, one’s eye is immediately drawn to the red line, which cuts the X-axis at 1 — representing 100% probability.
By zooming in on the range of 0 to 1, one is presented with the entire spectrum of probabilities from 0 to 100%. This graph is the key to unlocking the computation efficiencies of probability.

The graph above is used to represent the logarithmic probability associated with a percentage probability.
The graph above demonstrates the relationship between the x-axis (percentage) and the y-axis (logprob). When the probability is 1, the logprob is 0 and when the probability is 0.5, the logprob is approximately -0.7. This relationship can be seen clearly in the graph, and can be used to determine the logprob of any given percentage.
Logprobs are always negative numbers, and as the probability approaches zero the logprob increases exponentially. Crucially, these logprobs offer a significant computational advantage over the traditional use of percentages: by adding the logprobs together rather than multiplying the percentages, the same result is achieved, but with computational speed optimisation. This dramatically increases the efficiency of GPT.
Converting probability percentages to logprobs
By leveraging the natural logarithmic formula, one can mathematically convert a percentage to a logprob with ease.
To ascertain the logprob of 0.3, or 30%, you would apply the following formula:

The logprob of 30% is -1.20397.
In Ruby:
Math.log(0.3)
# Output: -1.20397
Converting Logprob to Percentage
To convert a logprob back into a percentage perform the inverse calculation which is the constant e to the power of the logprob. This will give us the probability percentage.
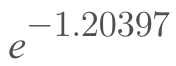
In Ruby we use the exponential method of the Math module. The exponential method uses the constant e as the base.
Math.exp(-1.20397)
# Output: 0.3
Adding Logprobs vs Multiplying Probability Percentages
The power of logprobs is in its computational efficiency.
Take the example prompt “What is AI?”. It is comprised of 4 tokens.

When this prompt is feed into GPT-3’s playground with a temperature of 0.7 we get the following response.

Under the hood, GPT needs to determine the probability of the token immediately following the question “What is AI?”. Statistically “AI” has an 85.35% probability of appearing after the prompt “What is AI?”.
The table below shows the probability percentage for each token as it appears successively after the preceding tokens.

Probability percentage of each token. Orange for token, green for response.
Note: The ‘What’ at the beginning of the prompt has no probability since it is the origin word of the prompt.
Mathematically to calculate the combined probability of the tokens occurring in this sequence you would multiply these probabilities together.
0.1892 * 0.0001 * 0.4550 * 0.9982 * 0.8535
# Output: 0.000007334
On the other hand by converting these values into logprobs we can arrive at the same answer by adding the logprobs together.

-1.665 + -9.210 + -0.787 + -0.002 + -0.158
# Output: -11.823
Math.exp(-11.823)
#Output: 0.000007334
Notice when the total logprob is converted back into a percentage it is identical to the product of the percentages calculated above.
Benchmarking multiplication vs addition in Ruby
This following performance test runs a comparison between the multiply and addition operations in Ruby.
I created two functions 1) multiplying a percentage together and 2) adding a logprob together — both 500 times. This would potentially simulate a 500 token response from GPT. This is looped 100,000 times to gain a statistically significant benchmark.
def benchmark_prob_multiplication
start_time = Time.now
100000.times do
500.times do
total =* 0.5
end
end
end_time = Time.now
puts "Multiply: Time elapsed #{(end_time - start_time)*1000} milliseconds"
end
def benchmark_logprob_addition
start_time = Time.now
100000.times do
500.times do
total =+ -0.693147
end
end
end_time = Time.now
puts "Addition: Time elapsed #{(end_time - start_time)*1000} milliseconds"
end
benchmark_prob_multiplication
benchmark_logprob_addition
Output:
#Multiply: Time elapsed 5558.755999999999 milliseconds
#Addition: Time elapsed 2979.3219999999997 milliseconds
As you can observe, logprob addition increases the speed of calculations by almost a factor of two. Taking into consideration the considerable amount of traffic handled by chatGPT alone, this improvement in computational efficiency is of great significance.
An interesting note, in the GPT playground, with “show probabilities” turned on, you are able to quickly calculate the total logprob of the entire prompt and response by highlighting the text.

Accessing token logprob via the API interface
With the GPT API you can access the response token logprobs in the JSON response. By adding the logprobs parameter you can see the logprob of the most likely tokens, as well as the chosen token. The logprobs parameter takes an integer from 1 to 5. If 5 is passed to the API endpoint the response will return the top 5 possible tokens for each token returned. 5 is the maximum value for this parameter.
require 'ruby/openai'
require 'json'
client = OpenAI::Client.new(access_token: '<YOUR_API_KEY>')
prompt = "What is AI?"
response = client.completions(
parameters: {
model: "text-davinci-003",
prompt: prompt,
temperature: 0.5,
max_tokens: 10,
logprobs: 1
}
)
response.to_json
puts response['choices'][0]['logprobs']
Output:
{
"tokens":[
"\n",
"\n",
"AI",
" (",
"Art",
"ificial",
" Intelligence",
")",
" is",
" a"
],
"top_logprobs":[
{
"\n":-0.001757213
},
{
"\n":-0.0023516808
},
{
"AI":-0.15741464
},
{
" (":-0.27175382
},
{
"Art":-0.18933135
},
{
"ificial":-0.0018770588
},
{
" Intelligence":-0.002153406
},
{
")":-0.0010475154
},
{
" is":-0.03325031
},
{
" a":-0.37541595
}
]
}
What can you do with logprobs
In the realm of natural language processing, the ability to control the response from GPT is a deft skill. With fine-grained control, repetition within a response can be greatly reduced or even eliminated. As an example, when the prompt “What is AI?” is posed, you may not want the model to repeat the word “AI”. To prevent this, the frequency parameter can be adjusted to decrease the logprob of the word to a point near 0.
Furthermore, the logprob can be used to compare various GPT outputs and select the one with the highest probability, or perhaps the lowest probability. This is especially useful when using the n parameter, which requests multiple responses from GPT. Through these methods, fine-grained control can be achieved to ensure an optimized response from GPT.
Conclusion
Logprobs are a sophisticated concept, but if you take the time to understand them, you will be rewarded with a level of control over GPT’s outputs that is truly impressive. As you deepen your exploration of GPT, you will find that the ability to work with logprobs can open up a whole new world of possibilities for your applications.
Kane Hooper is the CEO of reinteractive a specialist Ruby on Rails.
If you need any help with your Rails project you can contact Kane directly.
